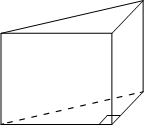
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
Объем прямой призмы равен произведению площади основания и высоты.
Высота известна, найдем площадь основания.
Площадь прямоугольного треугольника равна половине произведения катетов.
По теореме Пифагора найдем второй катет (обозначим его длину как x):
(√
34=9+x2
x2=34-9=25
x=5
Sоснования=3*5/2=15/2=7,5
V=7,5*6=45
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
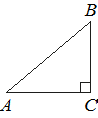В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
На координатной прямой отмечены точки A, B, C и D.
Число m равно √2.
Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
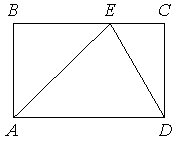На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.
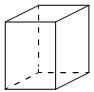Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: