Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?
Переведем условие задачи в математическую форму:
Пусть x - количество вопросов, на которые ученик дал правильные ответы.
y - количество вопросов, на которые ученик дал неправильные ответы.
Тогда можем составить уравнение:
7*x-12*y=70
Заметим, что "x" и "y" целые положительные числа, а "y" еще и неравна 0.
7*x=70+12*y
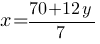
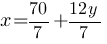
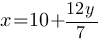
Напомним, что "x" и "y" целые числа, значит надо подобрать такое целое "y", чтобы "x" тоже был целым.
Так как дробь 12/7 сократить нельзя, и 7 является простым числом, то получается, что "y" должен быть кратен 7, т.е. 7, или 14, или 21 и т.д.
При y=7, x=10+12*7/7=22, т.е. 22 правильных ответа, 7 неправильных и 33-22-7=4 неотвеченых.
При y=14, x=10+12*14/7=34 - это невозможно, так как по условию всего вопросов 33.
Ответ: 22
Поделитесь решением
Присоединяйтесь к нам...
Найдите чётное трёхзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6000+4100n, где n — число колец, установленных при копании колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 4 колец. Ответ дайте в рублях.
Найдите значение выражения 38*10-1,3*102.
Сергей Петрович хочет купить в интернет-магазине микроволновую печь определённой модели. В таблице показано 6 предложений от разных интернет-магазинов.
| Номер магазина | Рейтинг магазина | Стоимость товара (руб.) | Стоимость доставки (руб.) |
| 1 | 4 | 17980 | 490 |
| 2 | 5 | 20490 | 500 |
| 3 | 4,5 | 18890 | 400 |
| 4 | 4 | 17490 | 0 |
| 5 | 3,5 | 13979 | 690 |
| 6 | 5 | 17750 | 600 |
Найдите значение выражения (√23+3)(√23-3).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: