
Постройте график функции
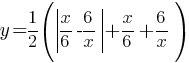
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Область Допустимых Значений (ОДЗ).
x≠0 (так как делить на ноль нельзя).
Так как функция содержит
модуль, то ее надо разложить на две подфункции:

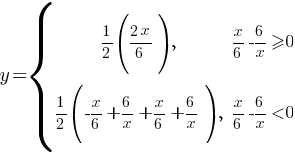
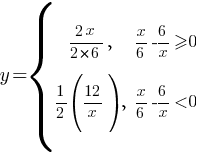
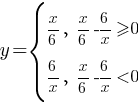
Теперь найдем для каких х 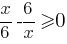 , а для каких х
, а для каких х 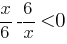
Найдем эти диапазоны.
Для начала преобразуем эту разность дробей, чтобы было легче проводить дальнейшие вычисления:
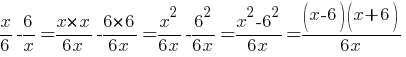
Последнее действие проводилось по формуле разность квадратов.
1) Рассмотрим первое неравенство 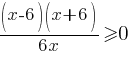 .
.
Дробь больше нуля в двух случаях:
a) Когда и числитель и знаменатель больше нуля.
b) Когда и числитель и знаменатель меньше нуля.
Рассмотрим вариант "а":
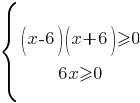
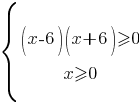
Чтобы решить систему неравенств нужно решить каждое неравенство по отдельности и пересечь полученные диапазоны.
Диапазон второго неравенства (0;+∞), а диапазон для первого неравенства найдем, решив уравнение (x-6)(x+6)=0
x1=6
x2=-6
 Коэффициент а=1, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Значит диапазон для первого неравенства:
Коэффициент а=1, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Значит диапазон для первого неравенства:
(-∞;-6]∪[6;+∞).
Пересекаем с диапазоном второго неравенства:
(-∞;-6]∪[6;+∞)∩(0;+∞)=[6;+∞)
Рассмотрим случай b), когда и числитель и знаменатель меньше нуля.
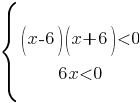
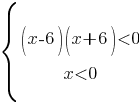
Эту систему решать не будем, а возьмем "обратные" диапазоны, т.е. для первого неравенства диапазон будет (-6;6), а для второго (-∞;0).
Пересекаем диапазоны:
(-6;6)∩(-∞;0)=(-6;0)
В итоге мы получили, что:
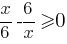 на диапазонах (-6;0) и [6;+∞)
на диапазонах (-6;0) и [6;+∞)
2) Рассмотрим второе неравенство 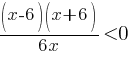 .
.
Решать это неравенство также не будем, а просто возьмем обратный диапазон от первого: (-∞;-6) и (0;6).
Запишем нашу первоначальную систему с полученными диапазонами:
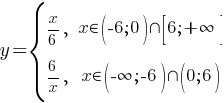
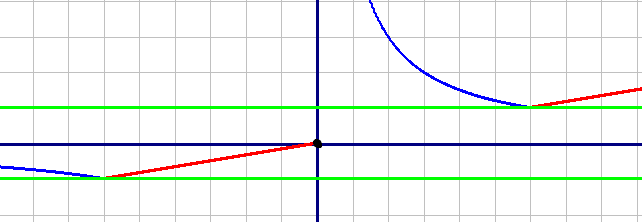 Построим графики функций.
Построим графики функций.
Красным цветом постоим первую функцию, которая является прямой, по точкам:
| X | -6 | 0 | 6 |
| Y | -1 | 0 | 1 |
| X | -12 | -6 | 1 | 6 |
| Y | -0,5 | -1 | 6 | 1 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
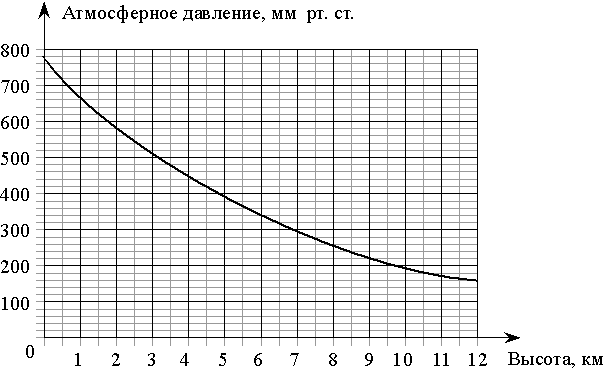 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
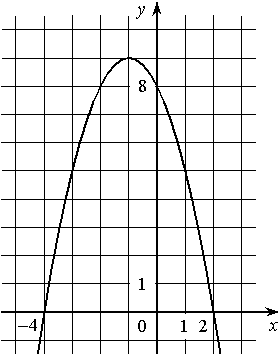 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке (-∞;-1]
2) Наибольшее значение функции равно 8
3) f(-4)≠f(2)
Постройте график функции y=2x+4|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
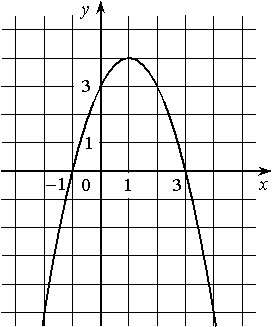 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(-1)=f(3)
2) Наибольшее значение функции равно 3
3) f(x)>0 при -1<x<3
Комментарии: