
Постройте график функции 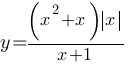 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Область Допустимых Значений (ОДЗ):
Так как присутствует деление на (х+1), х≠-1, так как деление на ноль невозможно.
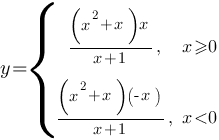
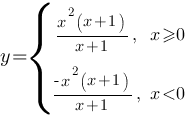
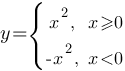
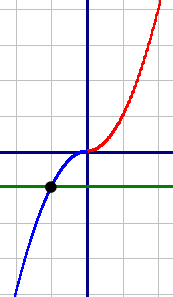 Построим график для каждой подфункции и объединим их.
Построим график для каждой подфункции и объединим их.| X | 0 | 1 | 2 | 3 |
| Y | 0 | 1 | 4 | 9 |
| X | 0 | -1 | -2 |
| Y | 0 | -1 | -4 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
 x2-10x+25, если x≥4,
x2-10x+25, если x≥4,
x-3, если x<4,
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=x+5|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции y=x2-3|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры в первой половине суток. Ответ дайте в градусах Цельсия.
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры в первой половине суток. Ответ дайте в градусах Цельсия.
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=-x2+2x+5
Б) y=x2+2x-5
В) y=-x2-2x+5
ГРАФИКИ
1) 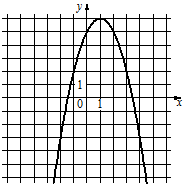 2)
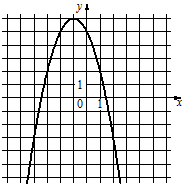
2) 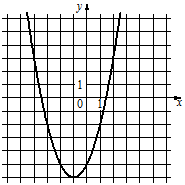 3)
3) 
В таблице под каждой буквой укажите соответствующий номер.
Комментарии: