
Решите систему уравнений 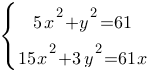
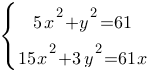
Умножим первое уравнение на 3:

Заметим, что левые части обоих уравнений полностью совпадают, т.е. равны. Следовательно и правые части уравнений равны между собой:
183=61x
x=3
Теперь подставим полученное значение "х" в любое из уравнений, например в первое:
5x2+y2=61
5*32+y2=61
45+y2=61
y2=61-45
y2=16
y2-16=0
Это квадратное уравнение можно решить через дискриминант, но в данном случае можно поступить проще, воспользоваться формулой разность квадратов:
y2-42=0
(y-4)(y+4)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому надо рассмотреть два варианта:
1) y-4=0 => y1=4
2) y+4=0 => y2=-4
Получаем две пары ответов: (3;4) и (3;-4).
Ответ: (3;4), (3;-4)
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение системы неравенств
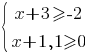
1) 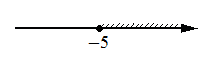
2) 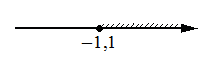
3) 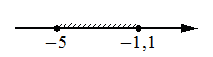
4) 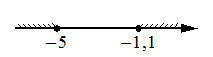
Решите уравнение 5x2-10x=0.
Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Первая труба пропускает на 6 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 140 литров она заполняет на 3 минуты дольше, чем вторая труба?
Средний вес мальчиков того же возраста, что и Саша, равен 66 кг. Вес Саши составляет 75% среднего веса. Сколько килограммов весит Саша?
Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
Комментарии: