
Решите уравнение 1/x2+2/x-3=0.
1/x2+2/x-3=0
Область Допустимых Значений (ОДЗ):
x≠0 (т.к. на ноль делить нельзя).
Приводим к общему знаменателю x2:
1/x2+2x/x2-3x2/x2=0
(1+2x-3x2)/x2=0
1+2x-3x2=0
Решим это
квадратное уравнение:
D=22-4*(-3)*1=4+12=16
x1=(-2+4)/(2*(-3))=2/(-6)=-1/3
x2=(-2-4)/(2*(-3))=(-6)/(-6)=1
Корни не пересекаются с ОДЗ.
Ответ: x1=-1/3,
x2=1
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений 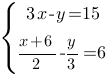
Известно, что число m отрицательное. На каком из рисунков точки с координатами 0, m, 2m, m2 расположены на координатной прямой в правильном порядке?
1) 
2) 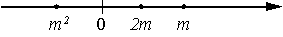
3) 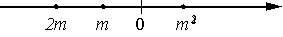
4) 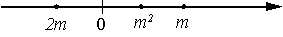
Решите уравнение x6=(7x-12)3.
Решите систему уравнений 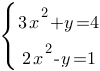
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 39 минут раньше, чем велосипедист приехал в А, а встретились они через 26 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
Комментарии:
(2017-05-29 00:00:10) Администратор: Наташа, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-05-23 20:48:28) Наташа: (2x-3/x²-4x+x - x-1\\x²-2x ) : x²-2/x³-4
(2017-05-23 20:47:33) Наташа: (2x-3/x²-4x+x - x-1\\x²-2x ) : x²-2/x³-4