
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 39 минут раньше, чем велосипедист приехал в А, а встретились они через 26 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
Обозначим:
Sм - путь, который проехал мотоциклист.
Sв - путь, который проехал велосипедист.
tм - время в пути мотоциклиста.
tв - время в пути велосипедиста.
vм - скорость мотоциклиста.
vв - скорость велосипедиста.
Sм=Sв (так как расстояние между городами величина постоянная)
tм=tв-39 минут
vм*26 - расстояние, которое проехал мотоциклист, от А до встречи
vв*26 - расстояние, которое проехал велосипедист, от В до встречи
vм*26+vв*26 - расстояние между городами, следовательно:
vм*26+vв*26=vв*tв
А так же vв*tв=vм*tм
Получаем систему:
 vм*26+vв*26=vв*tв
vм*26+vв*26=vв*tв
vв*tв=vм*(tв-39)
 vв*26-vв*tв=-vм*26
vв*26-vв*tв=-vм*26
vв*tв=vм*(tв-39)
 vв*(26-tв)=-vм*26
vв*(26-tв)=-vм*26
vв*tв=vм*(tв-39)
Разделим одно выражение на другое:
(26-tв)/tв=-26/(tв-39)
(26-tв)(tв-39)=-26tв
26tв-39*26-tв2+39tв=-26tв
tв2-26tв-26tв-39tв+1014=0
tв2-91tв+1014=0
Решим это
квадратное уравнение:
D=(-91)2-4*1*1014=8281-4056=4225
tв1=(-(-91)+65)/2=78
tв2=(-(-91)-65)/2=13
13 минут - не подходит для ответа, так как противоречит условию, что они встретились через 26 минут.
tв=78 минут = 1 час и 18 минут
18/60=0,3
Ответ: tв=1,3 часа
Поделитесь решением
Присоединяйтесь к нам...
Городской бюджет составляет 27 млн рублей, а расходы на одну из его статей составили 10%. Сколько рублей потрачено на эту статью бюджета?
Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решите систему неравенств 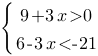
На каком рисунке изображено множество её решений?
1) 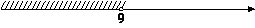
2) 
3) 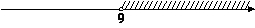
4) 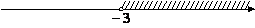
Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Решите уравнение 8-5(2x-3)=13-6x.
Комментарии:
(2014-05-12 22:40:48) Администратор: София, можно...Одну и ту же задачу можно решить несколькими способами. Например, существует несколько сотен доказательств теоремы Пифагора. На нашем сайте мы пытаемся решить задачу максимально просто, последовательно и понятно для учащихся, которые не силны в математике. Вы, я вижу, к таким не относитесь ). Огромное спасибо за Ваш интерес к нашему сайту и за Ваш вариант решения. Но наш вариант мне кажется более простым и универсальным. Мы с удовольствием разместим на сайте решения, которые окажутся короче или проще. Еще раз спасибо!!!
(2014-05-12 21:39:40) София: Можно так: Пусть скорость мотоциклиста х км в мин, скорость велосипедиста у км в мин. До встречи они ехали 26 минут Мотоциклист проехал От А до встречи М - 26 х км, велосипедист от В до встречи М 26 у км После встречи велосипедист ехал расстояние МА, 26 х км со скоростью у км в мин 26х/у минут ехал велосипедист А мотоциклист наоборот, ехал путь от М до В, 26 у км со скоростью х км в мин 26у/х минут По условию время велосипедиста на 39 минут больше 26х/у-39=26у/х получим уравнение 2х²-3ху-2у²=0 Раздели уравнение на у² х/у=z 2z²-3z-2=0 z=2 или z=-1|2 х/у=2 х=2у Велосипедист сначала ехал 26 минут, а потом проехал путь 26х со скоростью у, 26·2у/у=52 минуты Всего 26+52=78 минут ехал велосипедист 78 мин=1,3 ч Ответ: 1,3 ч