
Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
Обозначим v - скорость теплохода в неподвижное воде.
Тогда:
v+4 - скорость теплохода по течению
v-4 - скорость теплохода против течения
165/(v+4) - время движения теплохода по течению
165/(v-4) - время движения теплохода против течения
Запишем уравнение для времени:
165/(v+4)+165/(v-4)+5=18
Приведем к общему знаменателю:
(165(v-4))/((v-4)(v+4))+(165(v+4))/((v-4)(v+4))=18-5
(165(v-4)+165(v+4))/((v-4)(v+4))=13
(165v-660+165v+660)/(v2-42)=13
330v/(v2-16)=13
330v=13(v2-16)
0=13v2-330v-208
Решим квадратное уравнение через дискриминант:
D=(-330)2-4*13*(-208)=108900+10816=119716
√
v1=(-(-330)+346)/(2*13)=26
v1=(-(-330)-346)/(2*13)=-16/26
Отрицательной скорость быть не может, поэтому подходит только v=26
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.

Найдите наименьшее из чисел a2, a3, a4.
1) a2
2) a3
3) a4
4) не хватает данных для ответа
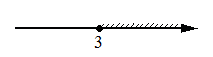
Укажите решение системы неравенств
 х-3,7≤0,
х-3,7≤0,
х-2≥1.
1) 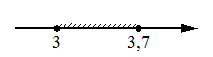
2) 
3) 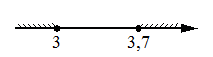
4) 
Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 13 рублей 80 копеек. Сколько процентов составляет скидка для пенсионера?
Решите систему неравенств 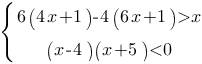
Укажите решение неравенства 4x-4≥9x+6.
1) [-0,4;+∞)
2) (-∞;-2]
3) [-2;+∞)
4) (-∞;-0,4]
Комментарии: