ОГЭ, Математика. Числовые последовательности: Задача №FD3153 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Числовые последовательности: Задача №FD3153

Задача №150 из 182
Условие задачи:

Геометрическая прогрессия задана условием b_n=164(1/2)ⁿ. Найдите сумму первых её 4 членов.

Решение задачи:

Вариант №1
Чтобы найти сумму первых 4 членов данной геометрической прогрессии, воспользуемся формулами. В нашем случае, удобней воспользоваться первой. Для этого необходимо узнать b₁ - первый член прогрессии и q - знаменатель прогрессии.
b₁=164*(1/2)¹=82 (из условия задачи). А q=1/2.
Тогда:

Ответ: S₄=153,75

Вариант №2
В данной задаче надо найти сумму всего четырех первых членов. Поэтому можно просто вычислить значения каждого члена и сложить их:
b₁=164(1/2)¹=164/2=82
b₂=164(1/2)²=164/4=41
b₃=164(1/2)³=164/8=20,5
b₄=164(1/2)⁴=164/16=10,25
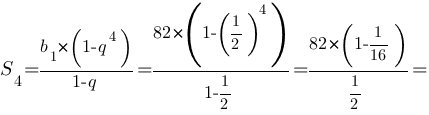
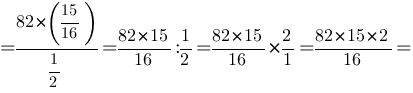
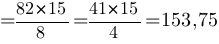
S₄=82+41+20,5+10,25=153,75
Ответ: 153,75

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №475D55

Последовательность (b_n) задана условиями b₁=-6, b_n+1=-2*(1/b_n). Найдите b₅.

Задача №9E3EDA

Выписаны первые три члена геометрической прогрессии:
-1024; -256; -64; …
Найдите сумму первых пяти её членов.

Задача №F8A2D4

Геометрическая прогрессия задана условиями b₁=-7, b_n+1=3b_n. Найдите сумму первых 5 её членов.

Задача №2A803D

Геометрическая прогрессия (b_n) задана условиями:
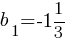, b_n+1=-3b_n.
Найдите b₇.

Задача №475D55

Последовательность (b_n) задана условиями b₁=-6, b_n+1=-2*(1/b_n). Найдите b₅.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X

Значение не введено

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.