Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=-x2-6,25 ровно одну общую точку. Постройте этот график и все такие прямые.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
y=-x2-6,25
y=kx
kx=-x2-6,25
x2+kx+6,25=0
Найдем корни этого
уравнения:
D=k2-4*1*6,25=k2-25
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=k2-25=0
k2=25
k1=5
k2=-5
Получаем функции:
y=-x2-6,25
y=5x
y=-5x
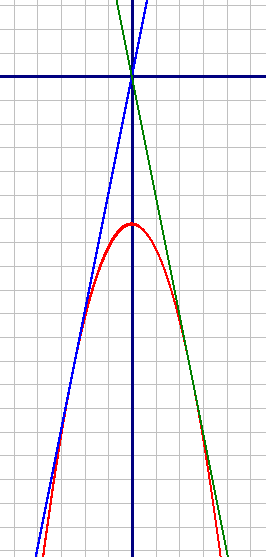построим графики по точкам:
y=-x2-6,25 (красный)
| X | -2 | -1 | 0 | 1 | 2 |
| Y | -10,25 | -7,25 | -6,25 | -7,25 | -10,25 |
| X | -1 | 0 | 1 |
| Y | -5 | 0 | 5 |
| X | -1 | 0 | 1 |
| Y | 5 | 0 | -5 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x2+3x-4|x+2|+2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=2x+4 2) y=-2x-4 3) y=2x-4 4) y=-2x+4 |
А)  |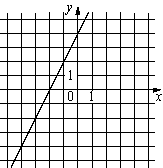
Б)  |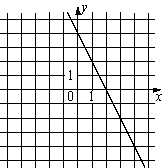
В)  |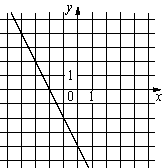
Постройте график функции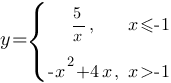 
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
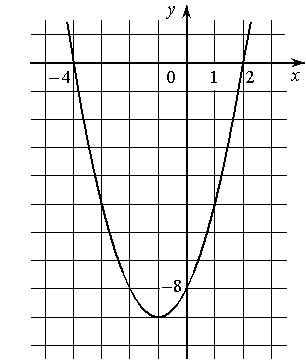На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) Функция убывает на промежутке [-1;+∞)
2) ƒ(x)>0 при x<-4 и при x>2
3) Наименьшее значение функции равно -9
Известно, что графики функций y=x2+p и y=-2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: