Решите уравнение (x2-36)2+(x2+4x-12)2=0.
Вариант №1
(x2-36)2+(x2+4x-12)2=0
(x2-36)2=-(x2+4x-12)2
Квадрат любого числа всегда больше или равен нулю, следовательно данное равенство возможно только когда
(x2-36)2=0
(x2+4x-12)2=0
Решим каждое равенство:
1) (x2-36)2=0
x2-36=0
x2=36
x1=6
x2=-6
2) (x2+4x-12)2=0
x2+4x-12=0
Решим это квадратное уравнение через дискриминант:
D=42-4*1*(-12)=16+48=64
x1=(-4+8)/(2*1)=4/2=2
x2=(-4-8)/(2*1)=-12/2=-6
Получаем, что только при x=-6 ОБА уравнения будут равняться нулю.
Ответ: -6
Поделитесь решением
Присоединяйтесь к нам...
Решите неравенство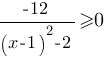 
Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
Поступивший в продажу в апреле мобильный телефон стоил 4800 рублей. В июле он стал стоить 4560 рублей. На сколько процентов снизилась цена на мобильный телефон в период с апреля по июль?
Решите систему уравнений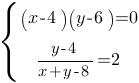 
На координатной прямой отмечено число c. Расположите в порядке убывания числа c, c2 и 1/c.
Хочу получать новые решения
Ни какого спама
Автор: Таська
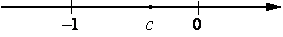
Комментарии:
(2024-04-16 20:36:42) Алина: (x²-36)²+(x²+14x+48)²=0