
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ256 –Є–Ј 1087 |
 –Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞
ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCP, —А–∞–≤–µ–љ 8, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ BAC —А–∞–≤–µ–љ 4/3. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞
ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCP, —А–∞–≤–µ–љ 8, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ BAC —А–∞–≤–µ–љ 4/3. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–†–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ R=(AC+CB-AB)/2. –Ф–ї—П —Н—В–Њ–≥–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –і–ї–Є–љ—Л –≤—Б–µ—Е —Б—В–Њ—А–Њ–љ –і–∞–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC.
–Я–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О tgBAC=CB/AC=4/3 => AC=3*CB/4=0,75*CB.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ AB2=AC2+CB2
AB2=(0,75*CB)2+CB2
AB2=1,5625*CB2
AB=1,25*CB
–Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М CB.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC:
/ABC=180°-90°-/BAC
–Ф–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BCP:
/ABC=180°-90°-/BCP
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, /BAC=/BCP.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCP.
–Я–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О tgBCP=BP/CP=4/3 => CP=3*BP/4=0,75*BP.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ CB2=CP2+BP2
CB2=(0,75*BP)2+BP2
CB2=1,5625*BP2
CB=1,25*BP
BP=0,8*CB
r=(BP+CP-CB)/2
2*r=BP+0,75*BP-CB
2*8=1,75*BP-CB
16=1,75*0,8*CB-CB
16=0,4*CB
CB=40
–Т—Л—З–Є—Б–ї–Є–≤ CB, –Љ—Л –Љ–Њ–ґ–µ–Љ –≤—Л—З–Є—Б–ї–Є—В—М AB –Є AC, —Г–Ї–∞–Ј–∞–љ–љ—Л–µ –≤—Л—И–µ:
AB=1,25*CB=1,25*40=50
AC=0,75*CB=0,75*40=30
R=(AC+CB-AB)/2, —В–Њ–≥–і–∞ –њ–Њ–ї—Г—З–∞–µ–Љ:
R=(30+40-50)/2=10.
–Ю—В–≤–µ—В: R=10.
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Э–∞ –Њ—В—А–µ–Ј–Ї–µ AB –≤—Л–±—А–∞–љ–∞ —В–Њ—З–Ї–∞ C —В–∞–Ї, —З—В–Њ AC=6 –Є BC=4. –Я–Њ—Б—В—А–Њ–µ–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ A, –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј C. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є, –њ—А–Њ–≤–µ–і—С–љ–љ–Њ–є –Є–Ј —В–Њ—З–Ї–Є B –Ї —Н—В–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–Э–∞ –Њ—В—А–µ–Ј–Ї–µ AB –≤—Л–±—А–∞–љ–∞ —В–Њ—З–Ї–∞ C —В–∞–Ї, —З—В–Њ AC=6 –Є BC=4. –Я–Њ—Б—В—А–Њ–µ–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ A, –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј C. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є, –њ—А–Њ–≤–µ–і—С–љ–љ–Њ–є –Є–Ј —В–Њ—З–Ї–Є B –Ї —Н—В–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
 –Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ NPQM –і–Є–∞–≥–Њ–љ–∞–ї—М NQ —П–≤–ї—П–µ—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є —Г–≥–ї–∞ PNM –Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В—Б—П —Б –і–Є–∞–≥–Њ–љ–∞–ї—М—О PM –≤ —В–Њ—З–Ї–µ S. –Э–∞–є–і–Є—В–µ NS, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Њ–Ї–Њ–ї–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ NPQM –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, PQ=44, SQ=16.
–Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ NPQM –і–Є–∞–≥–Њ–љ–∞–ї—М NQ —П–≤–ї—П–µ—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є —Г–≥–ї–∞ PNM –Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В—Б—П —Б –і–Є–∞–≥–Њ–љ–∞–ї—М—О PM –≤ —В–Њ—З–Ї–µ S. –Э–∞–є–і–Є—В–µ NS, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Њ–Ї–Њ–ї–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ NPQM –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, PQ=44, SQ=16.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, AC=8, cosA=0,4. –Э–∞–є–і–Є—В–µ AB.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, AC=8, cosA=0,4. –Э–∞–є–і–Є—В–µ AB.
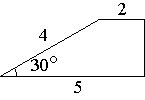 –С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 4, –∞ –Њ–і–Є–љ –Є–Ј –њ—А–Є–ї–µ–≥–∞—О—Й–Є—Е –Ї –љ–µ–є —Г–≥–ї–Њ–≤ —А–∞–≤–µ–љ
30¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –µ—Б–ї–Є –µ—С –Њ—Б–љ–Њ–≤–∞–љ–Є—П —А–∞–≤–љ—Л 2 –Є 5.
–С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 4, –∞ –Њ–і–Є–љ –Є–Ј –њ—А–Є–ї–µ–≥–∞—О—Й–Є—Е –Ї –љ–µ–є —Г–≥–ї–Њ–≤ —А–∞–≤–µ–љ
30¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –µ—Б–ї–Є –µ—С –Њ—Б–љ–Њ–≤–∞–љ–Є—П —А–∞–≤–љ—Л 2 –Є 5.
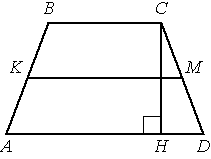 –Т —В—А–∞–њ–µ—Ж–Є–Є –Р–Т–°D –±–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —А–∞–≤–љ—Л, –°–Э вАФ –≤—Л—Б–Њ—В–∞, –њ—А–Њ–≤–µ–і—С–љ–љ–∞—П –Ї –±–Њ–ї—М—И–µ–Љ—Г –Њ—Б–љ–Њ–≤–∞–љ–Є—О AD. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ HD, –µ—Б–ї–Є —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П KM —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 10, –∞ –Љ–µ–љ—М—И–µ–µ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 4.
–Т —В—А–∞–њ–µ—Ж–Є–Є –Р–Т–°D –±–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —А–∞–≤–љ—Л, –°–Э вАФ –≤—Л—Б–Њ—В–∞, –њ—А–Њ–≤–µ–і—С–љ–љ–∞—П –Ї –±–Њ–ї—М—И–µ–Љ—Г –Њ—Б–љ–Њ–≤–∞–љ–Є—О AD. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ HD, –µ—Б–ї–Є —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П KM —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 10, –∞ –Љ–µ–љ—М—И–µ–µ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 4.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2015-10-13 13:48:55) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –°–≤–µ—В–ї–∞–љ–∞, –і–∞, –≤–Є–і–Є–Љ–Њ –Ї —Н—В–Њ–Љ—Г –Ј–∞–і–∞—З–∞ –Є —Б–≤–Њ–і–Є—В—Б—П, –љ–Њ —П –љ–µ –Љ–Њ–≥—Г –љ–∞–є—В–Є —В–µ–Њ—А–µ–Љ—Г (–Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ, —Б–≤–Њ–є—Б—В–≤–Њ), –≤ –Ї–Њ—В–Њ—А–Њ–Љ –±—Л —Г—В–≤–µ—А–ґ–і–∞–ї–Њ—Б—М, —З—В–Њ –≤ –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞—Е –Њ—В–љ–Њ—И–µ–љ–Є–µ —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О —А–∞–і–Є—Г—Б–Њ–≤ –≤–њ–Є—Б–∞–љ–љ—Л—Е –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є. –Р –µ—Б–ї–Є —Н—В–Њ –љ–Є–≥–і–µ –љ–µ –і–Њ–Ї–∞–Ј–∞–љ–Њ, —В–Њ –њ—А–Є–љ–Є–Љ–∞—В—М —Н—В–Њ –Ї–∞–Ї –і–∞–љ–љ–Њ—Б—В—М –љ–µ–ї—М–Ј—П. –Ь–Њ–ґ–µ—В –±—Л—В—М –Т—Л –њ–Њ–і—Б–Ї–∞–ґ–Є—В–µ, –≥–і–µ –Є—Б–Ї–∞—В—М?
(2015-10-11 19:13:12) –°–≤–µ—В–ї–∞–љ–∞: –њ—А–Њ—Й–µ —А–µ—И–Є—В—М –Ј–∞–і–∞—З—Г —З–µ—А–µ–Ј –њ–Њ–і–Њ–±–Є–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤:–Р–°–Т –Є –°–†–Т,–љ–∞–є—В–Є —Б–Є–љ—Г—Б–Р (—З—А–µ–Ј —В–∞–љ–≥–µ–љ—Б –љ–∞–є—В–Є –Ї–Њ—Б–Є–љ—Г—Б,–Ј–∞—В–µ–Љ —Б–Є–љ—Г—Б)–Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–Њ–і–Њ–±–љ—Л—Е —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–Њ —Б–Є–љ—Г—Б—Г= –Њ—В–љ–Њ—И–µ–љ–Є–µ —А–∞–і–Є—Г—Б–Њ–≤