Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Введем обозначения:
v - собственная скорость баржи.
v+5 - скорость баржи по течению.
v-5 - скорость баржи против течения.
t1 - время движения баржи по течению.
t2 - время движения баржи против течения.
Тогда получаем:
t1=40/(v+5)
t2=30/(v-5)
t1+t2=5
Подставляем значения t1 и t2 в последнее уравнение:
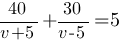
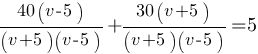
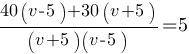
40v-200+30v+150=5
(v+5)(v-5)
70v-50=5(v2-52) - разделим левую и правую части уравнения на 5
14v-10=v2-52
0=v2-25-14v+10
v2-14v-15=0
Решим это
квадратное уравнение через
дискриминант:
D=(-14)2-4*1*(-15)=196+60=256
v1=(-(-14)+16)/(2*1)=(14+16)/2=30/2=15 км/ч
v2=(-(-14)-16)/(2*1)=(14-16)/2=-2/2=-1 км/ч
Так как скорость отрицательной быть не может, то:
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
Магазин детских товаров закупает погремушки по оптовой цене 240 рублей за одну штуку и продаёт с 20-процентной наценкой. Сколько рублей будут стоить 4 такие погремушки, купленные в этом магазине?
О числах a и c известно, что a<c. Какое из следующих неравенств неверно
1) a+8<c+8
2) -a/33<-c/33
3) a-2<c-2
4) -a/33<c/33
Решите уравнение 9/(x-2)=9/2.
Решите неравенство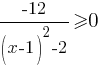 
Найдите наибольшее значение x, удовлетворяющее системе неравенств
Хочу получать новые решения
Ни какого спама
Автор: Таська
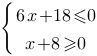
Комментарии: