Два автомобиля одновременно отправляются в 560-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
Обозначим:
v - скорость первого автомобиля.
v-10 - скорость второго автомобиля.
t - время первого автомобиля.
t+1 - время второго автомобиля.
Получаем два уравнения:
v*t=560 - для первого автомобиля.
(v-10)(t+1)=560 - для второго автомобиля.
Выразим t через v в первом уравнении:
t=560/v
И подставим его во второе уравнение:
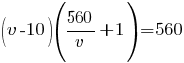
Раскроем скобки:
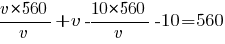
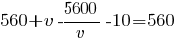
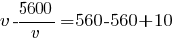
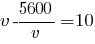
Умножим все уравнение на v:
v2-5600=10v
v2-10v-5600=0
Решим это квадратное уравнение через дискриминант:
D=(-10)2-4*1*(-5600)=100+22400=22500
v1=(-(-10)+150)/(2*1)=(10+150)/2=160/2=80
v2=(-(-10)-150)/(2*1)=(10-150)/2=-140/2=-70
Так как скорость не может быть отрицательной, то остается только один вариант.
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
Решение какого из данных неравенств изображено на рисунке?
1) x2-49<0
2) x2+49>0
3) x2+49<0
4) x2-49>0
Решите систему уравнений 
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Из пунктов А и В, расстояние между которыми 19 км, одновременно навстречу друг другу вышли два туриста и встретились в 10 км от В. Турист, шедший из А, сделал в пути получасовую остановку. Найдите скорость туриста, шедшего из В, если известно, что он шёл со скоростью, на 1 км/ч меньшей, чем турист, шедший из А.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: