
Решение какого из данных неравенств изображено на рисунке?

1) x2-7x<0
2) x2-49>0
3) x2-7x>0
4) x2-49<0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен единице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 3) будут совпадать, т.к. это одинаковые функции.
- графики парабол 2) и 4) будут совпадать, т.к. это одинаковые функции.
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть 0 и 7.
 Решим уравнение x2-7x=0
Решим уравнение x2-7x=0
x(x-7)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому:
1) x1=0
2) x-7=0 => x2=7
Посмотрим на рисунок, в условии показаны диапазоны, когда график функции выше оси Х, т.е. больше нуля, следовательно, подходит неравенство x2-7x>0
Проверим уравнение x2-49=0
x2-72=0
(x-7)(x+7)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому:
1) x-7=0 => x1=7
2) x+7=0 => x2=-7
Корни не совпали с указанными на рисунке, следовательно неравенства x2-49 не подходят.
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему неравенств 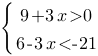
На каком рисунке изображено множество её решений?
1) 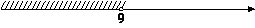
2) 
3) 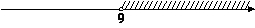
4) 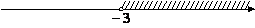
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
В начале года число абонентов телефонной компании «Запад» составляло 800 тыс. человек, а в конце года их стало 920 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Решите систему уравнений 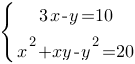
Решите систему неравенств 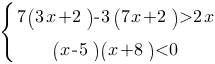
Комментарии: