Дана геометрическая прогрессия (bn), знаменатель которой равен 1/2, b1=2. Найдите сумму первых 4 её членов.
Вариант №1 (по формуле)
Воспользуемся первой формулой:
S4=b1(1-q4)/(1-q)=2*(1-(1/2)4)/(1-1/2)=2*(1-0,0625)/(1/2)=1,875/(0,5)=3,75
Ответ: 3,75
Вариант №2 ("в лоб")
Если необходимо просуммировать небольшое количество членов, то можно воспользоваться методом "в лоб", т.е. сначала вычислить все 4 члена, а потом сложить их.
b1=2
b2=b1*q=2*1/2=1
b3=1*1/2=1/2
b4=(1/2)*1/2=1/4
S4=b1+b2b3+b4=2+1+1/2+1/4=3+0,5+0,25=3,75
Ответ: 3,75
Поделитесь решением
Присоединяйтесь к нам...
Последовательность (bn) задана условиями: b1=4,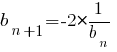 
Найдите b3.
Геометрическая прогрессия задана условием bn=160*3n. Найдите сумму первых её 4 членов.
Дана арифметическая прогрессия (an), разность которой равна -4,9, a1=-0,2. Найдите a7.
Геометрическая прогрессия задана условиями b1=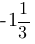
, bn+1=-3bn. Найдите b7.
Дана арифметическая прогрессия (an), для которой a10=19, a15=44. Найдите разность прогрессии.
Хочу получать новые решения
Ни какого спама
Автор: Таська
,
Комментарии: