ОГЭ, Математика. Числовые последовательности: Задача №24B689 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Числовые последовательности: Задача №24B689

Задача №69 из 182
Условие задачи:

Выписаны первые несколько членов геометрической прогрессии: 17; 68; 272; ... Найдите её четвёртый член.

Решение задачи:

В геометрической прогрессии зависимость членов прогрессии можно записать так: b_n+1=b_nq
Тогда:
b₂=b₁q
68=17q
q=4
b₄=b₃q=272*4=1088
Ответ: b₄=1088

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №17C33D

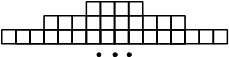Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 6 квадратов больше, чем в предыдущей. Сколько квадратов в 53-й строке?

Задача №E53FE9

Выписаны первые несколько членов геометрической прогрессии: 1512; -252; 42; … Найдите сумму первых четырёх её членов.

Задача №C61C01

Последовательность задана условиями b₁=-3, b_n+1=-3*1/b_n. Найдите b₄.

Задача №AEC6A3

Дана геометрическая прогрессия (b_n), знаменатель которой равен 1/2, b₁=2. Найдите сумму первых 4 её членов.

Задача №4BA08B

Дана арифметическая прогрессия (a_n), разность которой равна -4,9, a₁=-0,2. Найдите a₇.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Геометрическая прогрессия — последовательность чисел b₁, b₂, b₃,...(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где b₁≠0, q≠0: b₁, b₂=b₁q, b₃=b₂q,...,b_n=b_n-1q
Любой член геометрической прогрессии может быть вычислен по формуле: b_n=b₁q^n-1

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.