Геометрическая прогрессия задана условиями b1=-6, bn+1=2bn. Найдите b6.
По условию задачи
геометрическая прогрессии задана условием: bn+1=2bn,
следовательно
b2=2b1, т.е. q=2.
b6=b1q5
b6=-6*25=-6*32=-192
Ответ: b6=-192
Поделитесь решением
Присоединяйтесь к нам...
Арифметическая прогрессия (an) задана условиями: a1=3, an+1=an+4. Найдите a10.
Геометрическая прогрессия задана условиями b1=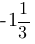
, bn+1=-3bn. Найдите b7.
Дана арифметическая прогрессия (an), для которой a6=-7,8, a19=-10,4. Найдите разность прогрессии.
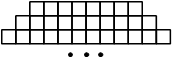Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 117-й строке?
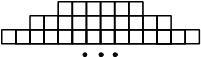Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 4 квадрата больше, чем в предыдущей. Сколько квадратов в 54-й строке?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-03-15 19:11:18) Администратор: Карина, посмотрите задачу №148 в этом же разделе. Она очень похожа на Вашу.
(2018-03-12 15:48:20) карина: Выписано несколько последовательных членов геометрической прогрессии: … ; -12 ; x ; -3 ; 1,5 ; … Найдите член прогрессии, обозначенный буквой x