ОГЭ, Математика. Числовые последовательности: Задача №1625CE | Ответ-Готов 


Юмор

Автор: Таська
Так выглядит современная программа обучения.
...читать далее

ОГЭ/ГИА

ЕГЭ (базовый уровень)

Числа и вычисления

Алгебраические выражения

Уравнения и неравенства

Числовые последовательности

Функции

Координаты на прямой и плоскости

Геометрия

Статистика и теория вероятностей

Алгебра

Уравнения и неравенства

Функции

Начала математического анализа

Геометрия

Элементы комбинаторики, статистики и теории вероятностей

ОГЭ, Математика.
Числовые последовательности: Задача №1625CE

Задача №65 из 182
Условие задачи:

Последовательность задана условиями a1=3, an+1=an+4. Найдите a10.

Решение задачи:

Данная последовательность - арифметическая.
В условии сказано:
an+1=an+4
an+1-an=4=d - это разность прогрессии.
Любой член арифметической прогрессии можно выразить через a1:
an=a1+(n-1)d, тогда:
a10=a1+(10-1)d=3+9*4=3+36=39
Ответ: 39

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела



Задача №3CC264

Записаны первые три члена арифметической прогрессии: -9; -5; -1. Какое число стоит в этой арифметической прогрессии на 91-м месте?



Задача №DC2B3F

Арифметическая прогрессия (an) задана условиями:
a1=48, an+1=an-17.
Найдите сумму первых семи её членов.



Задача №4C6ABB

Дана арифметическая прогрессия (an), разность которой равна -4,9, a1=-6,4. Найдите a15.



Задача №E67F92

Геометрическая прогрессия задана условиями b1=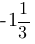, bn+1=-3bn. Найдите b7.



Задача №FD3153

Геометрическая прогрессия задана условием bn=164(1/2)n. Найдите сумму первых её 4 членов.

Комментарии:


(2015-05-11 13:53:57) Администратор: Диана, а дополнил решение. По определению d=an+1-an.
(2015-05-11 06:27:00) Диана: Почему d=4?

Найти задачу

По номеру с сайта fipi.ru (шестизначный номер из букв и цифр)
По порядковому номеру в текущем разделе
(от 1 до 182)
По словам
Искать во всех разделах

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки
X Арифметическая прогрессия - числовая последовательность вида a1, a1+d, a1+2d,..., a1+(n-1)d,...то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d (шага, или разности прогрессии):
an=an-1+d
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
an=a1+(n-1)d, где a1 - первый член последовательности, d - ее разность.
X

Задайте вопрос по этой задаче.

Ваше имя:


Рейтинг@Mail.ru Copyright otvet-gotov.ru 2014-2021. Все права защищены. Яндекс.Метрика