Арифметическая прогрессия (an) задана условиями:
a1=48, an+1=an-17.
Найдите сумму первых семи её членов.
Вариант №1 (по формуле)
Вычислим разность арифметической прогрессии:
d=an+1-an=-17 (по условию задачи).
Используем формулу для нахождения суммы членов прогрессии:
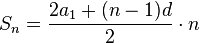
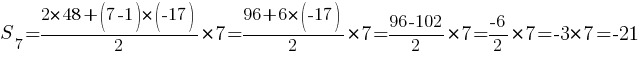
Ответ: -21
Поделитесь решением
Присоединяйтесь к нам...
Геометрическая прогрессия задана условием bn=-77*2n. Найдите сумму первых её 5 членов.
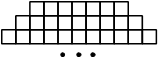Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 39-й строке?
Выписаны первые несколько членов арифметической прогрессии: 6; 8; 10; … Найдите сумму первых шестидесяти её членов.
Записаны первые три члена арифметической прогрессии: -8; -1; 6. Какое число стоит в этой арифметической прогрессии на 51-м месте?
Выписаны первые три члена геометрической прогрессии:
125; -100; 80; …
Найдите её пятый член.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: