Выписаны первые несколько членов арифметической прогрессии: 1; 3; 5; … Найдите сумму первых шестидесяти её членов.
Чтобы найти сумму
арифметической прогрессии у нас есть
две формулы.
Вариант 1 (по первой формуле)
Для этого найдем d - разность прогрессии.
d=a2-a1=3-1=2.
Найдем a60:
a60=a1+(n-1)d=1+(60-1)2=119
Ответ: 3600
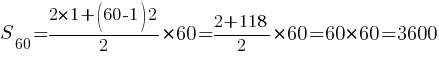
Поделитесь решением
Присоединяйтесь к нам...
Геометрическая прогрессия задана условием bn=164(1/2)n. Найдите сумму первых её 4 членов.
Выписаны первые несколько членов арифметической прогрессии: 6; 10; 14; … Найдите сумму первых пятидесяти её членов.
В геометрической прогрессии сумма первого и второго членов равна 160, а сумма второго и третьего членов равна 40. Найдите первые три члена этой прогрессии.
Дана арифметическая прогрессия (an), разность которой равна 7, a1=9,4. Найдите a13.
Выписаны первые несколько членов арифметической прогрессии: 1, 3, 5, … Найдите её одиннадцатый член.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-11-13 21:30:48) Администратор: Ольга, я сделал решение более читабельным. Надеюсь вопросы сняты.
(2017-11-10 18:39:40) Ольга: А как получили 30 ?!