Дана арифметическая прогрессия (an), для которой a10=19, a15=44. Найдите разность прогрессии.
Любой член
арифметической прогрессии можно записать через первый член прогрессии (a1) и разность прогрессии:
an=a1+(n-1)d
a10=a1+(10-1)d
19=a1+9d
19-9d=a1
a15=a1+(15-1)d
44=a1+14d
44=19-9d+14d
44-19=5d
25=5d
d=5
Ответ: 5
Поделитесь решением
Присоединяйтесь к нам...
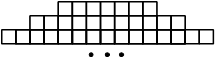Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 34-й строке?
Дана геометрическая прогрессия (bn) , знаменатель которой равен 5, b1=2/5. Найдите сумму первых 6 её членов.
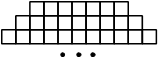Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 34-й строке?
Дана геометрическая прогрессия (bn) , знаменатель которой равен 5, b1=2/5. Найдите сумму первых 6 её членов.
Выписано несколько последовательных членов арифметической прогрессии: …; 1; x; -5; -8; … Найдите член прогрессии, обозначенный буквой x.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-04-19 21:00:19) Администратор: Лиза, рад, что Вы разобрались самостоятельно.
(2018-04-17 18:35:14) лиза : а все поняла
(2018-04-17 18:34:35) лиза: откуда взялось 44