
Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
Рассмотрим каждое утверждение.
1) "У
равнобедренного треугольника есть ось симметрии", это утверждение верно, ось совпадает с
высотой, опущенной к основанию треугольника.
2) "Если в
параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат", это утверждение верно, т.к. оно совпадает со
свойством квадрата.
3) "Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности", это утверждение неверно, окружности не будут пересекаться, если, например, центры окружностей совпадают.
Поделитесь решением
Присоединяйтесь к нам...
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
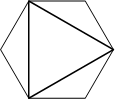 Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
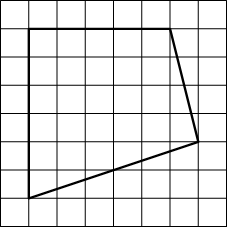 Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
 Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Комментарии: