В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
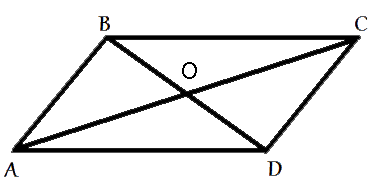Рассмотрим треугольники ABC и ACD.
Сторона AC - общая для этих треугольников, AB=CD и BC=AD (по
свойству параллелограмма), следовательно рассматриваемые треугольники равны (по
третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
Рассмотрим треугольник ACD, как только что выяснили, площадь этого треугольника равна половине площади параллелограмма. Отрезок DO - является
медианой (по третьему
свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади (
свойство медианы).
Следовательно площадь COD равна половине площади треугольника ACD. SCOD=SACD/2=SABCD/4.
Поделитесь решением
Присоединяйтесь к нам...
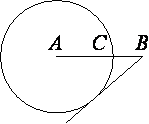На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
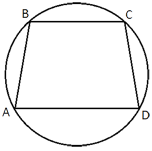Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
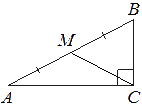В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
Хочу получать новые решения
Ни какого спама
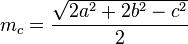, где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон: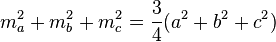 
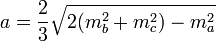, где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника. 
Автор: Таська
Комментарии: