Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны", это утверждение верно (по
признаку параллельности прямых)
2) "Диагональ
трапеции делит её на два равных треугольника." Во-первых, нет такого
свойства трапеции.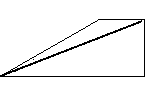 
Во-вторых, если рассмотреть
прямоугольную трапецию с
проведенной диагональю, то становится очевидным, что один из получившихся треугольников -
прямоугольный, а второй - нет.
Следовательно, это утверждение неверно.
3) "Если в
ромбе один из углов равен
90°, то такой ромб — квадрат". Чтобы ромб был квадратом, необходимо, чтобы все 4 угла были равны 90°.
Т.к.
ромб - частный случай
параллелограмма, то к нему и применимы все
свойства параллелограмма, следовательно (по
свойству параллелограмма), противоположный прямому углу, угол тоже равен 90°.
Другие два угла по тому же свойству равны друг другу.
Сумма углов многоугольника вычисляется по формуле (n-2)*180°, где n - количество углов. В нашем случае, углов - 4. Тогда сумма углов равна (4-2)*180°=360°.
Тогда получается, что сумма двух неизвестных углов равна 360°-90°-90°=180°. А так как они равны друг другу, то каждый из них равен 180°/2=90°.
Т.е. мы узнали, что все четыре угла равны по 90°, следовательно это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Площадь ромба равна 30, а периметр равен 24. Найдите высоту ромба.
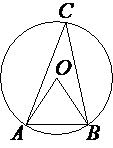Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
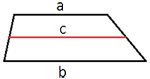
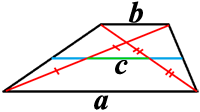
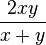(среднее гармоническое), где x и y — основания трапеции (формула Буракова).
Автор: Таська
Комментарии:
(2015-04-11 12:09:16) Администратор: Света, спасибо за уточнение, исправлено.
(2015-04-11 00:21:53) света: по 1)-это признак параллельности прямых ,а не свойство