
 На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Рассмотрим треугольник АВЕ.
/B=90° (т.к. ABCD -
прямоугольник).
/EAB=45° (по условию задачи).
Тогда по
теореме о сумме углов треугольника /BEA=180°-/B-/EAB=180°-90°-45°=45°.
Следовательно, треугольник ABE -
равнобедренный (по
свойству). Тогда AB=BE (по
определению равнобедренного треугольника).
EC=BC-BE=17-12=5 (т.к. BC=AD).
Рассмотрим треугольник ECD.
Он
прямоугольный (т.к. угол С - прямой).
Тогда по
теореме Пифагора получаем:
ED2=CD2+EC2
ED2=122+52
ED2=144+25=169
ED=13
Ответ: ED=13
Поделитесь решением
Присоединяйтесь к нам...
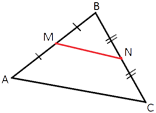 Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
 В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
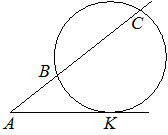 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
 На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
Комментарии: