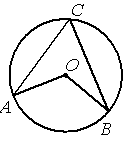
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=65°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 65°*2=130°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=130°.
Ответ: /AOB=130°.
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
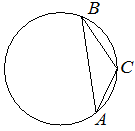В треугольнике ABC угол C равен 120°, AB=22√3. Найдите радиус окружности, описанной около этого треугольника.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
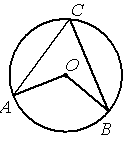Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: