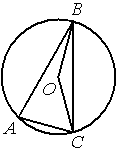
Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=75°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 75°*2=150°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=150°.
Ответ: /BOC=150°.
Поделитесь решением
Присоединяйтесь к нам...
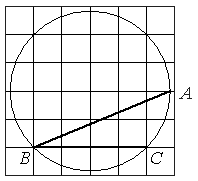Найдите угол ABC. Ответ дайте в градусах.
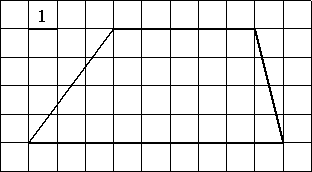Найдите площадь трапеции, изображённой на рисунке.
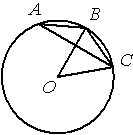Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
3) Площадь круга меньше квадрата длины его диаметра.
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: