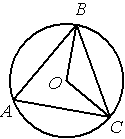
Точка О – центр окружности, /BAC=60° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=60°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 60°*2=120°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=120°.
Ответ: /BOC=120°.
Поделитесь решением
Присоединяйтесь к нам...
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=22.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 21°?
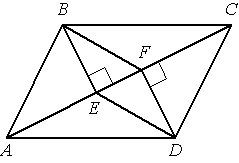В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: