
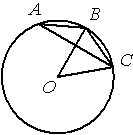
 Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=10°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 10°*2=20°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=20°.
Ответ: /BOC=20°.
Поделитесь решением
Присоединяйтесь к нам...
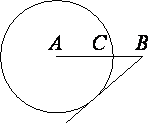 На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
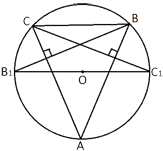 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
 Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
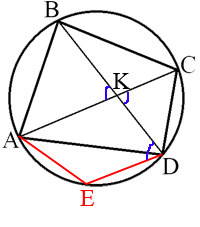 Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Дуга, на которую опирается центральный угол имеет ту же градусную меру.
Дуга, на которую опирается центральный угол имеет ту же градусную меру.
Комментарии: