Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Рассмотрим каждое утверждение:
1) "Центры
вписанной и описанной окружностей
равнобедренного треугольника совпадают." - это утверждение неверно, т.к. центр вписанной окружности находится внутри треугольника, а центр описанной окружности может находиться вне треугольника (по
теореме об окружности).
2) "Существует
параллелограмм, который не является
прямоугольником." - это утверждение верно, т.к. не противоречит
определению параллелограмма.
3) "Сумма углов
тупоугольного треугольника равна 180°." - это утверждение верно, т.к. не противоречит
теореме о сумме углов треугольника.
Поделитесь решением
Присоединяйтесь к нам...
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
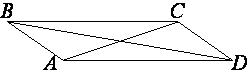В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
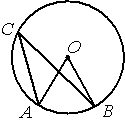Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: