На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, высота фонаря 9 м?
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE, эти треугольники
подобны, т.к. /C - общий, /B и /DEC - прямые, а углы A и EDC - равны, так как являются
соответственними.
Из подобия этих треугольников следует, что AB/DE=BC/EC,
AB/DE=(BE+EC)/EC, отсюда (AB*EC)/DE=BE+EC
BE=(AB*EC)/DE-EC
BE=(9*1)/1,8-1=4
Ответ: расстояние от фонаря до человека 4 м.
Поделитесь решением
Присоединяйтесь к нам...
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24. Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
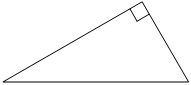Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
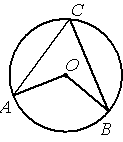Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
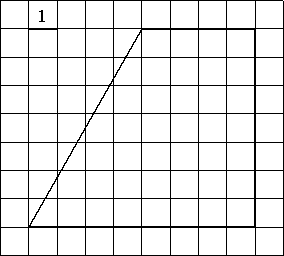Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: