Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Рассмотрим каждое утверждение:
1) "Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника".
Высота, проведенная к основанию является и
медианой, и биссектрисой (по
свойству равнобедренного треугольника), т.е. является
серединным перпендикуляром. А центром описанной окружности является точка пересечения
серединных перпендикуляров (
теорема об описанной окружности). Следовательно, это утверждение верно.
2) "Квадрат является прямоугольником", это утверждение верно (по
определению).
3) "Сумма углов любого треугольника равна 180°", это утверждение верно (по
теореме).
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен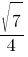 
. Найдите CosA.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Основания равнобедренной трапеции равны 3 и 17, боковая сторона равна 25. Найдите длину диагонали трапеции.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: