
 Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Площадь
ромба равна S=ah, где a - сторона ромба, h - высота ромба.
AD=AH+HD=21+8=29.
AD=AB=BC=CD (по
определению ромба).
Рассмотрим треугольник ABH.
ABH -
прямоугольный (т.к. BH -
высота), тогда по
теореме Пифагора: AB2=BH2+AH2
292=BH2+212
841=BH2+441
BH2=400
BH=20
Sромба=AD*BH=29*20=580
Ответ: Sромба=580
Поделитесь решением
Присоединяйтесь к нам...
 Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
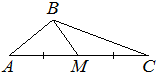 В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.
В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
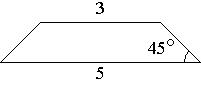 В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Комментарии: