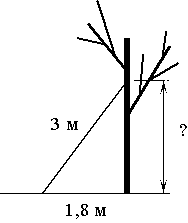
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Обозначим высоту, на которой находится конец лестницы, как Х. По
теореме Пифагора
32=1,82+X2
9=3,24+X2
X2=9-3,24
X2=5,76
X=2,4
Ответ: высота равна 2,4 метра.
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 50√
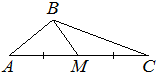В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
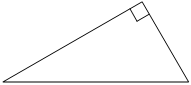В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: