Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту.
По
определению cos(/CDE)=ED/CD
3/5=ED/14
ED=3*14/5=8,4
По
теореме Пифагора:
CD2=ED2+EC2
142=8,42+EC2
196=70,56+EC2
EC2=125,44
EC=11,2 - это и есть высота
Sтрапеции=EC*(BC+AD)/2
Sтрапеции=11,2*(5+40)/2
Sтрапеции=5,6*45=252
Ответ: Sтрапеции=252
Поделитесь решением
Присоединяйтесь к нам...
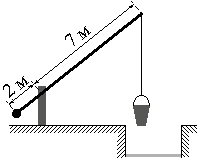На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
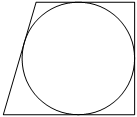Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
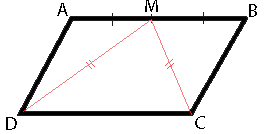В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
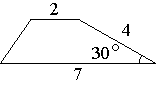Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: