
 В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
 Проведем высоты как показано на рисунке. И рассмотрим треугольник CDF. Это
прямоугольный треугольник (т.к. /CFD - прямой).
Проведем высоты как показано на рисунке. И рассмотрим треугольник CDF. Это
прямоугольный треугольник (т.к. /CFD - прямой).
По
теореме о сумме углов треугольника найдем угол FCD
/FCD=180°-90°-45°=45°. Заметим, что /FCD=/FDC. Следовательно, треугольник
равнобедренный (по
свойству равнобедренного треугольника). Отсюда следует, что FD=FC (по
определению равнобедренного треугольника).
Рассмотрим треугольник ABE. /BAE=/FDC=45° (т.к. по условию задачи
трапеция равнобедренная).
Аналогично по
теореме о сумме углов треугольника получим, что /ABE=180°-90°-45°=45°, а следовательно (аналогично предыдущему треугольнику) треугольник ABE -
равнобедренный.
Причем эти треугольники равны (AB=CD, BE=CF и /ABE=/FCD -
первый признак равенства)=> AE=FD.
Рассмотрим четырехугольник BCFE.
Т.к. BC||EF, BE и FC - высоты, следовательно /BEF=90°=/CFE. /EBC=/BCF=90°. Следовательно четырехугольник BCFE -
прямоугольник => BC=EF.
Теперь можем записать:
AD=AE+EF+FD, 8=AE+2+FD, 8=AE+2+AE
6=2*AE => AE=3.
Т.к. AE=BE=3, а BE-высота трапеции, то теперь можем вычислить
площадь трапеции.
Sтрапеции=(BC+AD)/2*BE
Sтрапеции=(2+8)/2*3=15.
Ответ: Sтрапеции=15.
Поделитесь решением
Присоединяйтесь к нам...
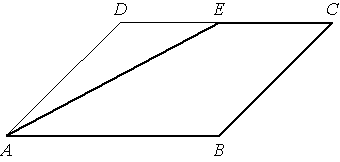 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
 Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Комментарии:
(2015-04-12 14:12:34) Администратор: Раньше мы доказали что треугольники ABE и DCF равны, поэтому FD=AE. Цитата из решения "Причем эти треугольники равны (AB=CD, BE=CF и /ABE=/FCD - первый признак равенства)=> AE=FD."
(2015-04-12 14:03:16) : непонятно , почему там fd ПРЕВРАТИЛОСЬ В AE?Теперь можем записать: AD=AE+EF+FD, 8=AE+2+FD, 8=AE+2+AE