
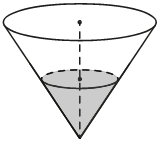
 В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
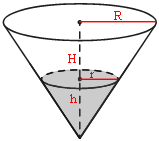 Рассмотрим треугольники, которые образуют:
Рассмотрим треугольники, которые образуют:
1) R-радиус основания сосуда, H-высота сосуда и боковая сторона сосуда
2) r-радиус конуса, образованный жидкостью, h-высота этого же конуса и боковая сторона этого конуса
Нижний угол этих треугольников общий.
Углы, образованные радиусами и высотами, прямые.
Следовательно, по первому признаку подобия треугольников эти треугольники
подобны.
Тогда, мы можем записать:
H/h=R/r
Из условия нам известно, что h=H/2, следовательно r=R/2.
Так как сосуд имеет вид конуса, то его объем мы можем записать так:
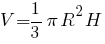
Соответственно, объем жидкости, которая тоже имеет форму конуса, мы запишем так:
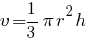
Подставляем значения r и h, выраженные через R и H.
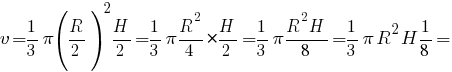
Заметим, все весь результат, кроме 1/8, это объем сосуда, т.е. можем записать:
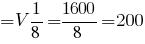
Ответ: 200
Поделитесь решением
Присоединяйтесь к нам...
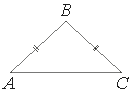 В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30°.
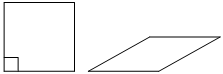 Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 16.
Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 16.
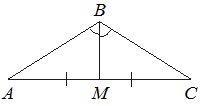 В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
 Аквариум имеет форму прямоугольного параллелепипеда
с размерами 80 см x 30 см x 40 см. Сколько литров составляет объём аквариума?
Аквариум имеет форму прямоугольного параллелепипеда
с размерами 80 см x 30 см x 40 см. Сколько литров составляет объём аквариума?
В одном литре 1000 кубических сантиметров.
Комментарии: