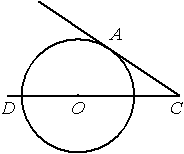
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
110°.
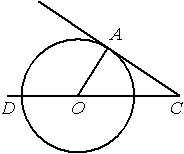Проведем отрезок ОА.
/DOA -
центральный угол для данной окружности. Он опирается на дугу AD, равную 110°. Следовательно, /DOA тоже равен 110°.
/AOC -
смежный углу DOA, поэтому /AOC=180°- /DOA=180°-110°=70°.
Треугольник ACO -
прямоугольный, т.к. радиус всегда перпендикулярен
касательной (по
свойству касательной). Т.е. /ОАС=90°. Применяя
теорему о сумме углов треугольника, можем записать:
180°=/AСO+/CAO+/AOC.
/AСO=180°-/CAO-/AOC=180°-90°-70°=20°.
Ответ: /ACO=20°.
Поделитесь решением
Присоединяйтесь к нам...
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
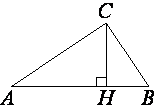В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
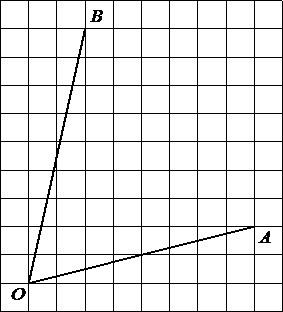Найдите тангенс угла
AOB.
Стороны AC, AB, BC треугольника ABC равны 3√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: