Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
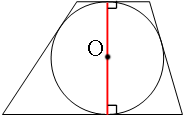Проведем радиусы к точкам касания с основаниями трапеции.
По первому свойству касательной (основания трапеции), она перпендикулярна радиусу.
Так как радиусы одновременно перпендикулярны параллельным основаниям трапеции, то получается, что радиусы представляют из себя единый отрезок или диаметр (это можно доказать если рассмотреть углы при параллельных прямых и секущей. Прямые углы являются односторонними и их сумма равна 180°).
Диаметр и является высотой трапеции:
h=D=2*R=2*24=48
Ответ: 48
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
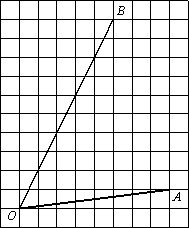Найдите тангенс угла AOB, изображённого
на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: