
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ97 –Η–Ζ 1087 |
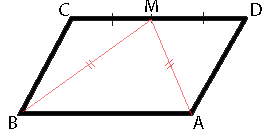 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD ―²–Ψ―΅–Κ–Α M βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ CD. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ MA=MB. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD ―²–Ψ―΅–Κ–Α M βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ CD. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ MA=MB. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η BCM –Η MDA. CM=MD, ―².–Κ. ―²–Ψ―΅–Κ–Α M - ―¹–Β―Ä–Β–¥–Η–Ϋ–Α CD, MA=MB (–Η–Ζ ―É―¹–Μ–Ψ–≤–Η―è –Ζ–Α–¥–Α―΅–Η), CB=AD (–Ω–Ψ ―¹–≤–Ψ–Ι―¹―²–≤―É –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α). –Γ–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ, ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η BCM –Η MDA ―Ä–Α–≤–Ϋ―΄ (–Ω–Ψ ―²―Ä–Β―²―¨–Β–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Α ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤).
–‰–Ζ ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Α ―ç―²–Η―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ /BCM=/MDA.
BC||AD (–Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α), ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ―É CD –Κ–Α–Κ ―¹–Β–Κ―É―â―É―é –Κ ―ç―²–Η–Φ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ. –Δ–Ψ–≥–¥–Α –Ω–Ψ–Μ―É―΅–Α–Β―²―¹―è, ―΅―²–Ψ ―¹―É–Φ–Φ–Α ―É–≥–Μ–Ψ–≤ BCM –Η MDA ―Ä–Α–≤–Ϋ–Α 180¬Α, ―².–Κ. ―ç―²–Η ―É–≥–Μ―΄ ―è–≤–Μ―è―é―²―¹―è –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Η–Φ–Η –Ψ–¥–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Η–Φ–Η. –û―²―¹―é–¥–Α ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ –Κ–Α–Ε–¥―΄–Ι –Η–Ζ ―ç―²–Η―Ö ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ 90¬Α.
–Δ–Β–Ω–Β―Ä―¨ ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD, –Ψ–Ϋ–Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ (―²–Ψ–Ε–Β –Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α). –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ―É BC –Κ–Α–Κ ―¹–Β–Κ―É―â―É―é –Κ ―ç―²–Η–Φ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ.
/CBA –Η /MCB - –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Η–Β –Ψ–¥–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Η–Β. –Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ –Η―Ö ―¹―É–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Α 180¬Α. –ê ―²–Α–Κ –Κ–Α–Κ /MCB=90¬Α, ―²–Ψ /CBA ―²–Ψ–Ε–Β ―Ä–Α–≤–Β–Ϋ 90¬Α.
–ê–Ϋ–Α–Μ–Ψ–≥–Η―΅–Ϋ–Ψ –¥–Ψ–Κ–Α–Ζ―΄–≤–Α–Β―²―¹―è, ―΅―²–Ψ /DAB ―²–Ψ–Ε–Β ―Ä–Α–≤–Β–Ϋ 90¬Α.
–ü–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ, ―É –Κ–Ψ―²–Ψ―Ä–Ψ–≥–Ψ –≤―¹–Β ―É–≥–Μ―΄ –Ω―Ä―è–Φ―΄–Β (―².–Β. 90¬Α) –Ϋ–Α–Ζ―΄–≤–Α–Β―²―¹―è –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–Φ (–Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é).
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
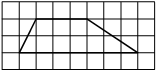 –ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β ―¹ ―Ä–Α–Ζ–Φ–Β―Ä–Ψ–Φ –Κ–Μ–Β―²–Κ–Η 1x1 –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η―è. –ù–Α–Ι–¥–Η―²–Β –Β―ë –Ω–Μ–Ψ―â–Α–¥―¨.
–ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β ―¹ ―Ä–Α–Ζ–Φ–Β―Ä–Ψ–Φ –Κ–Μ–Β―²–Κ–Η 1x1 –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η―è. –ù–Α–Ι–¥–Η―²–Β –Β―ë –Ω–Μ–Ψ―â–Α–¥―¨.
 –£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AD=3, BC=1, –Α –Β―ë –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 12. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AD=3, BC=1, –Α –Β―ë –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 12. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
 –Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ AOB, ―Ä–Α–≤–Ϋ―΄–Ι
60¬Α, –Ψ–Ω–Η―Ä–Α–Β―²―¹―è –Ϋ–Α ―Ö–Ψ―Ä–¥―É –ê–£ –¥–Μ–Η–Ϋ–Ψ–Ι 3. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η.
–Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ AOB, ―Ä–Α–≤–Ϋ―΄–Ι
60¬Α, –Ψ–Ω–Η―Ä–Α–Β―²―¹―è –Ϋ–Α ―Ö–Ψ―Ä–¥―É –ê–£ –¥–Μ–Η–Ϋ–Ψ–Ι 3. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η.
 –ë–Ψ–Κ–Ψ–≤―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 12 –Η 15, –Α –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β BC ―Ä–Α–≤–Ϋ–Ψ 3. –ë–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α ADC –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―¹–Β―Ä–Β–¥–Η–Ϋ―É ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–ë–Ψ–Κ–Ψ–≤―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 12 –Η 15, –Α –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β BC ―Ä–Α–≤–Ϋ–Ψ 3. –ë–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α ADC –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―¹–Β―Ä–Β–¥–Η–Ϋ―É ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η.
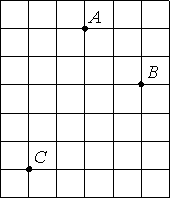 –ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β ―¹ ―Ä–Α–Ζ–Φ–Β―Ä–Ψ–Φ –Κ–Μ–Β―²–Κ–Η 1―¹–Φ ―Ö 1―¹–Φ –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A, B –Η C. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η A –¥–Ψ ―¹–Β―Ä–Β–¥–Η–Ϋ―΄ –Ψ―²―Ä–Β–Ζ–Κ–Α BC. –û―²–≤–Β―² –≤―΄―Ä–Α–Ζ–Η―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
–ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β ―¹ ―Ä–Α–Ζ–Φ–Β―Ä–Ψ–Φ –Κ–Μ–Β―²–Κ–Η 1―¹–Φ ―Ö 1―¹–Φ –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A, B –Η C. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η A –¥–Ψ ―¹–Β―Ä–Β–¥–Η–Ϋ―΄ –Ψ―²―Ä–Β–Ζ–Κ–Α BC. –û―²–≤–Β―² –≤―΄―Ä–Α–Ζ–Η―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: