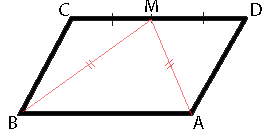
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники BCM и MDA. CM=MD, т.к. точка M - середина CD, MA=MB (из условия задачи), CB=AD (по свойству параллелограмма). Соответственно, треугольники BCM и MDA равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /BCM=/MDA.
BC||AD (по определению параллелограмма), рассмотрим сторону CD как секущую к этим параллельным сторонам. Тогда получается, что сумма углов BCM и MDA равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны AB и CD, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону BC как секущую к этим параллельным сторонам.
/CBA и /MCB - внутренние односторонние. Следовательно их сумма равна 180°. А так как /MCB=90°, то /CBA тоже равен 90°.
Аналогично доказывается, что /DAB тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Площадь прямоугольного треугольника равна
338√
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: