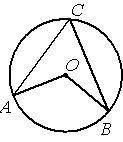
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=70°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 70°*2=140°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=140°.
Ответ: /AOB=140°.
Поделитесь решением
Присоединяйтесь к нам...
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
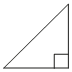В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 5 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: