
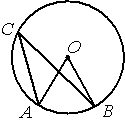
 Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=32°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 32°*2=64°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=64°.
Ответ: /AOB=64°.
Поделитесь решением
Присоединяйтесь к нам...
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=11, CK=20.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=11, CK=20.
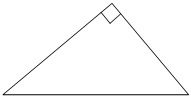 Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
Комментарии: