Стороны AC, AB, BC треугольника ABC равны 3√
По условию задачи /KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 3√
По условию задачи треугольник KAC подобен исходному треугольнику ABC. А значит углы этих треугольников соответственно равны (по определению подобных треугольников). Поэтому наибольшие углы двух рассматриваемых треугольников равны, т.е. /KAC=/ABC. /ACK не равен /ACB ( т.к. KC пересекает сторону AB в точке, отличной от B), поэтому /ACK = /BAC. Следовательно, /AKC=/ACB => cos(/AKC)=cos(/ACB).
Применяя теорему косинусов мы можем записать AB2=AC2+BC2-2*AC*BC*cos(/ACB).
(√
11=9*2+1-6*√
11-19=-6*√
8=6*√
cos(/AKC)=cos(/ACB)=8/(6*√
cos(/AKC)=cos(/ACB)=4/(3*√
cos(/AKC)=2/3*√
Ответ: cos(/AKC)=2/3*√
Поделитесь решением
Присоединяйтесь к нам...
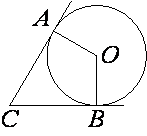В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Синус острого угла A треугольника ABC равен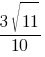 
. Найдите CosA.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: