
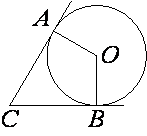 В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
Рассмотрим четырехугольник AOBC.
∠C=83° (по условию задачи).
∠CAO=∠CBO=90° (по
первому свойству касательной).
Сумма любого n-угольника равна (n-2)180°, значит сумма углов четырехугольника равна:
(4-2)180°=360°
Т.е. ∠C+∠CAO+∠CBO+∠AOB=360°
83°+90°+90°+∠AOB=360°
∠AOB=360°-83°-90°-90°
∠AOB=97°
Ответ: 97
Поделитесь решением
Присоединяйтесь к нам...
 Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
 Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
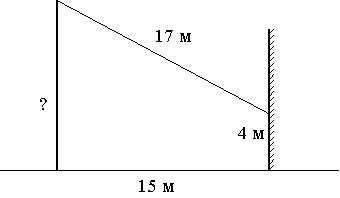 От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Комментарии:
(2021-10-27 18:20:41) Лена : центр окружности описанной треуг АВС лежит на стороне АВ Найти Угол АВС если угол ВАС равен 30