К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
Проведем отрезок ОВ.
Отрезок OB - это радиус окружности и этот отрезок перпендикулярен AB (по
свойству
касательной).
Следовательно, треугольник AOB -
прямоугольный, тогда, по
теореме Пифагора:
AO2=AB2+OB2
752=212+OB2
5625=441+OB2
OB2=5184
OB=72=R
Ответ: 72
Поделитесь решением
Присоединяйтесь к нам...
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
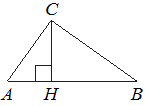На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-02-14 01:23:05) : Через концы А, В хорды окружности проведены касательные АС и ВС. Угол АСВ равен 130°. Найдите градусную величину меньшей дуги окружности, которая стягивается хордой АВ. В ответ запишите только число.