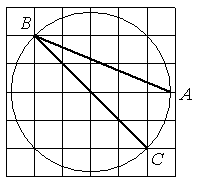
Найдите угол ABC. Ответ дайте в градусах.
Угол ABC (обозначим его α) является
вписанным в окружность, следовательно, он равен половине центрального угла, опирающегося на ту же дугу 2α (по
теореме).
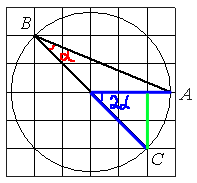Найдем
центральный угол через тангенс. Рассмотрим
центральный ("синий") угол и проведенный в нем катет ("зеленый").
tg(2α)=2/2=1
По
таблице угол 2α=45°
α=45°/2=22,5°
Ответ: 22,5
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
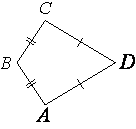В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP.
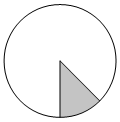Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=10:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: