
 В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
По второму свойству четырехугольника:
AB+CD=BC+AD=24
По
определению средней линии трапеции: m=(BC+AD)/2=24/2=12
Ответ: m=12
Поделитесь решением
Присоединяйтесь к нам...
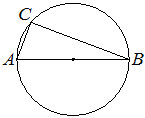 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 512√
Площадь прямоугольного треугольника равна 512√
 В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
 Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
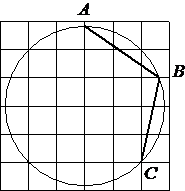 Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
Комментарии: