
 Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Рассмотрим рисунок:
BD - человек
AE - высота фонаря
ED - расстояние от фонаря до человека
DC - длина тени человека
Рассмотрим треугольники ACE и BCD.
∠C - общий
∠AEC=∠BDC=90° (это прямые углы)
Следовательно, по
первому признаку подобия треугольников, эти треугольники
подобны.
Тогда:
AE/BD=EC/DC
AE/BD=(ED+DC)/DC
7,2/1,8=(6+DC)/DC
4=6/DC+1
3=6/DC
DC=6/3=2
Ответ: 2 м.
Поделитесь решением
Присоединяйтесь к нам...
 Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
 ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
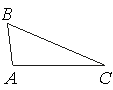 В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=32, MD=8, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=32, MD=8, H — точка пересечения высот треугольника ABC. Найдите AH.
 Площадь прямоугольного треугольника равна 578√
Площадь прямоугольного треугольника равна 578√
Комментарии:
(2016-10-29 11:49:48) Администратор: Кристина, (6+DC)/DC=6/DC+DC/DC=6/DC+1
(2016-10-29 11:21:57) Кристина: как из выражения 6+DC/DC у нас получается 6/DC+1?